Julio J. Candanedo

I am an AI scintist at SparseTrace. Prior, I was a postdoctoral researcher in the Department of Physics at University of Wisconsin-Milwaukee. I received my Ph.D. in 2023 from the Department of Physics at Arizona State University, advised by Professor John C.H. Spence, Oliver Beckstein, and Christian Arenz. My research lies broadly at the intersection of Physics and AI, with a current focus on physical chemistry, manifold learning, autoregressive generative models, and diffusion models.

email · github · google scholar · arXiv ·

Papers

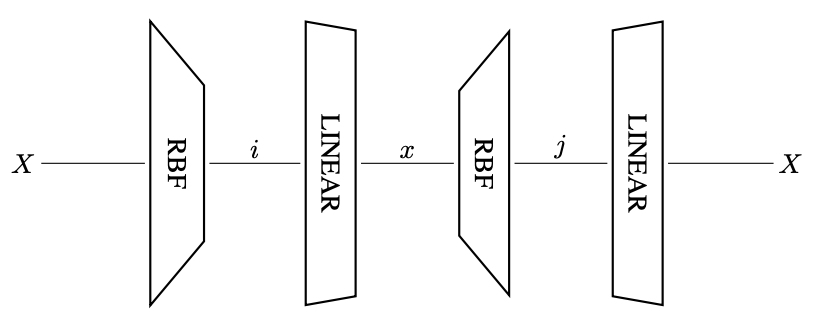
Linearized Diffusion Map

J. Candanedo · arXiv (2025)

arXiv code project page

We introduce the Linearized Diffusion Map (LDM), a novel linear dimensionality reduction method constructed via a linear approximation of the diffusion-map kernel. LDM integrates the geometric intuition of diffusion-based nonlinear methods with the computational simplicity, efficiency, and interpretability inherent in linear embeddings such as PCA and classical MDS. Through comprehensive experiments on synthetic datasets (Swiss roll and hyperspheres) and real-world benchmarks (MNIST and COIL-20), we illustrate that LDM captures distinct geometric features of datasets compared to PCA, offering complementary advantages. Specifically, LDM embeddings outperform PCA in datasets exhibiting explicit manifold structures, particularly in high-dimensional regimes, whereas PCA remains preferable in scenarios dominated by variance or noise. Furthermore, the complete positivity of LDM’s kernel matrix allows direct applicability of Non-negative Matrix Factorization (NMF), suggesting opportunities for interpretable latent-structure discovery. Our analysis positions LDM as a valuable new linear dimensionality reduction technique with promising theoretical and practical extensions.

E(3) Invariant Representations of Biomolecules

J. Candanedo · arXiv preprint (2025)

bioRxiv slides video

We present a coordinate-independent method for encoding protein structures using anchor-point-based trilateration that respects Euclidean symmetry while avoiding O(N^2) scaling problems of distance matrices. Our approach achieves near-perfect reconstruction of protein structures, and when combined with dimensionality reduction techniques, effectively captures conformational dynamics in molecular trajectories.

notes on Generalized Configuration-Interaction in python

J. Candanedo · chemRxiv preprint (2023)

chemRxiv slides video

In this work we construct a detailed understanding of the distribution of electrons as described by the Full-Configuration-Interaction (FCI) and for a generalized active-space. These results are presented at an introductory level for beginning practitioners or non-experts. Suitable background are a knowledge of linear-algebra and basic NumPy and Python principles of array manipulation.